题目背景

NOIP2018 提高组 D1T3

题目描述

C 城将要举办一系列的赛车比赛。在比赛前，需要在城内修建 $m$ 条赛道。

C 城一共有 $n$ 个路口，这些路口编号为 $1,2,…,n$，有 $n-1$ 条适合于修建赛道的双向通行的道路，每条道路连接着两个路口。其中，第 $i$ 条道路连接的两个路口编号为 $a_i$ 和 $b_i$，该道路的长度为 $l_i$。借助这 $n-1$ 条道路，从任何一个路口出发都能到达其他所有的路口。

一条赛道是一组互不相同的道路 $e_1,e_2,…,e_k$，满足可以从某个路口出发，依次经过 道路 $e_1,e_2,…,e_k$（每条道路经过一次，不允许调头）到达另一个路口。一条赛道的长度等于经过的各道路的长度之和。为保证安全，要求每条道路至多被一条赛道经过。

目前赛道修建的方案尚未确定。你的任务是设计一种赛道修建的方案，使得修建的 $m$ 条赛道中长度最小的赛道长度最大（即 $m$ 条赛道中最短赛道的长度尽可能大）

输入格式

输入文件第一行包含两个由空格分隔的正整数 $n,m$，分别表示路口数及需要修建的 赛道数。

接下来 $n-1$ 行，第 $i$ 行包含三个正整数 $a_i$,$b_i$,$l_i$，表示第 $i$ 条适合于修建赛道的道 路连接的两个路口编号及道路长度。保证任意两个路口均可通过这 $n-1$条道路相互到达。每行中相邻两数之间均由一个空格分隔。

输出格式

输出共一行，包含一个整数，表示长度最小的赛道长度的最大值。

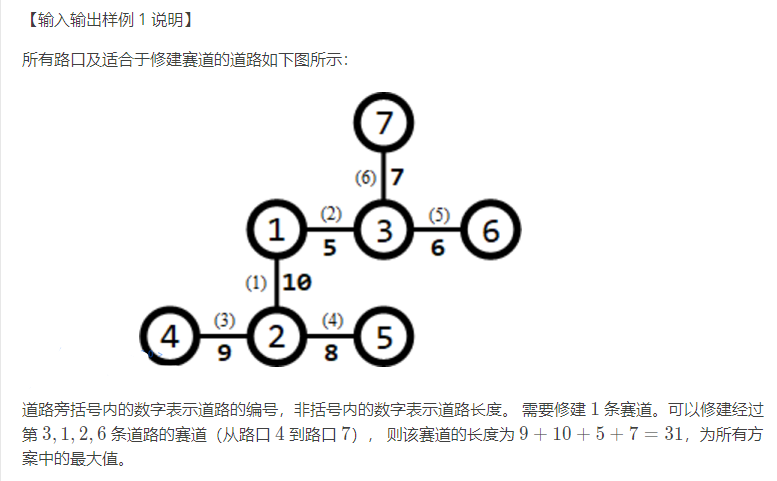
7 1 
1 2 10 
1 3 5 
2 4 9 
2 5 8 
3 6 6 
3 7 7

31

7 1 
1 2 10 
1 3 5 
2 4 9 
2 5 8 
3 6 6 
3 7 7

31

说明

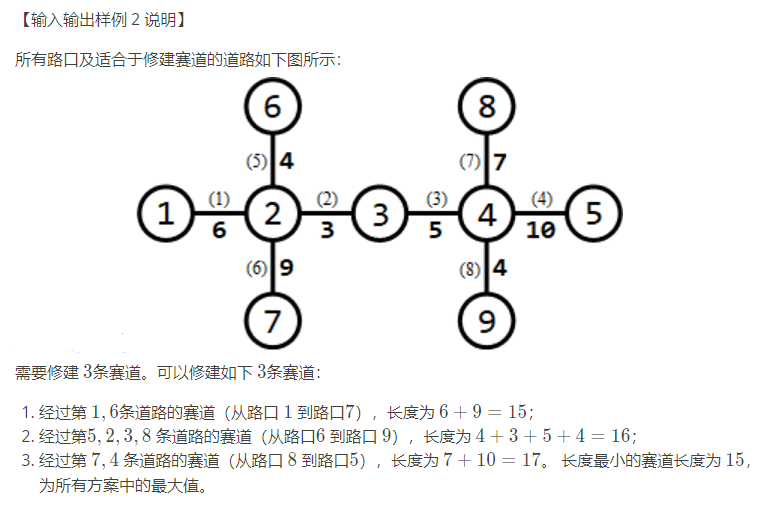
数据规模与约定

所有测试数据的范围和特点如下表所示 :

测试点编号	$n$	$m$	$a_i=1$	$b_i=a_i+1$	分支不超过 $3$
$1$	$\le 5$	$=1$	否	否	是
$2$	$\le 10$	$\le n-1$		是
$3$	$\le 15$		是	否	否
$4$	$\le 10^3$	$=1$	否		是
$5$	$\le 3\times 10^4$		是		否
$6$			否
$7$		$\le n-1$	是
$8$	$\le 5\times 10^4$
$9$	$\le 10^3$		否	是	是
$10$	$\le 3\times 10^4$
$11$	$\le 5\times 10^4$
$12$	$\le 50$			否
$13$
$14$	$\le 200$
$15$
$16$	$\le 10^3$
$17$					否
$18$	$\le 3\times 10^4$
$19$
$20$	$\le 5\times 10^4$

其中，「分支不超过 $3$」的含义为：每个路口至多有 $3$ 条道路与其相连。

对于所有的数据，$2 \le n \le 5\times 10^4, \ 1 \le m \le n − 1,\ 1 \le a_i,b_i \le n,\ 1 \le l_i \le 10^4$。